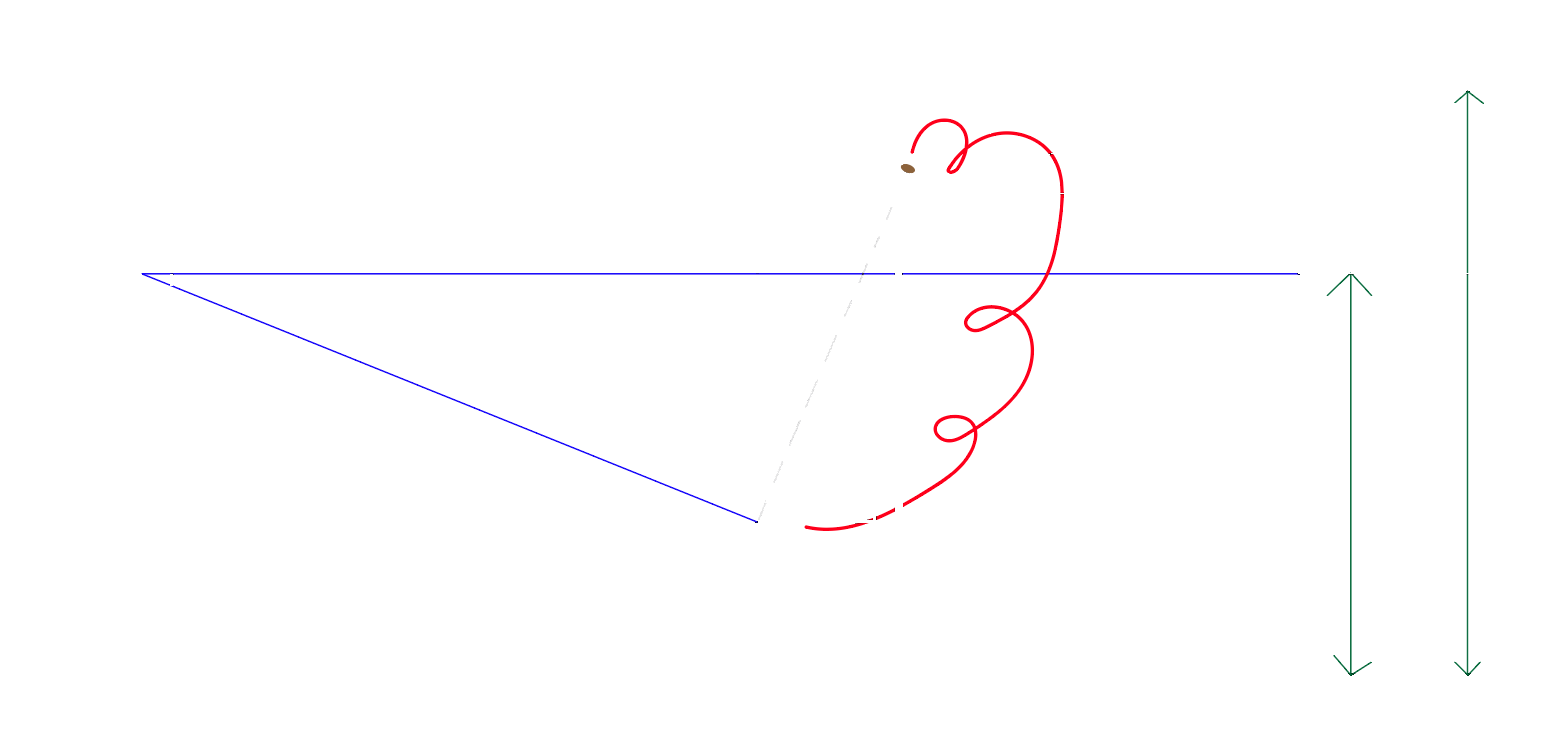
John is looking down from the top of a very tall building and sees a car 650m from the base of the building, and it is at an angle of depression of 47° to him at point C. Someone pushes him off and now his current location is point D. He calculates that the car is now at an angle of depression of 28° to him and he sees a bird at point E exactly 445m away from his starting point. Given this information, calculate the following:
- How far has John fallen so far (2 d.p.)
- What is the angle of elevation from John at point D to the bird? (nearest degree)
1b. John tripping and stabbing himself
John (J) was walking home from the shops where he bought a knife. While walking home he tripped over and threw his knife (K) up in the air. A random person was exactly 1.9km away horizontally was watching at this time, the angle of depression to the tip of John's head (D) is 30° and directly in front of him was 1.7km up a 5km building whose base was where John was standing. From the base of the building (G) to the top of the knife (K) is the angle of 40°, the knife is 2.5km away from the building horizontally and 0.4 km away from John horizontally. The knife if travelling at a constant angle towards John's head.
What is the angle of elevation from John's head to the knife? (nearest degree)
Refer to the diagram.
2a. John in a plane crash
John is catching a plane. The plane took off at point C at an angle of 30° and flew at that angle for 70km to point A. At point A the plane stalled and started to descend, at that angle of depression the plane will crash into the ground at point B in 60km and John will die.
Find the angle of depression from A to B. (nearest degree)
2b. John falling from a plane
John falls out of a plane which is travelling parallel to the ground at a constant velocity of 288 km/h. After 27 seconds John reached terminal velocity of 54m/s. At that exact time the angle of elevation from John to the plane is 23° and angle of depression from the plane to the desert directly below John is 70°.
How many seconds does John have to live? (2 d.p.)
3a. John crushed by a grand piano
John is walking on a street. From high above him, a person pushes a grand piano over a balcony, crushing John. John is about halfway under the piano (AB is half the piano's length).
If John is 5.84 ft tall, what is the angle from his head to the top of the piano (∠BCD). (nearest minute)
Use ft x 30.48 = cm for conversion
3b. John caught in a shootout
An armed robber robs a convenience store. Two police officers corner the man as he is stepping out of the store. The man then threatens to shoot John, who is in the store at the time. The officers, not wanting a hostage situation, shoot at the man, accidentally missing and hitting John.
How much did each officer miss by? (nearest minute)
(The distance between Officer 2 and John is twice the distance between Officer 1 and point I)
4a. John walking home
After somehow surviving falling out of a plane without a parachute, John is lost in the desert 3427 km west from his house, and his house is at a bearing of 147°.
If John walks at a constant pace of 5km/h, calculate how long it would take John to walk back home in hours if he took the most direct route. (2 d.p.)
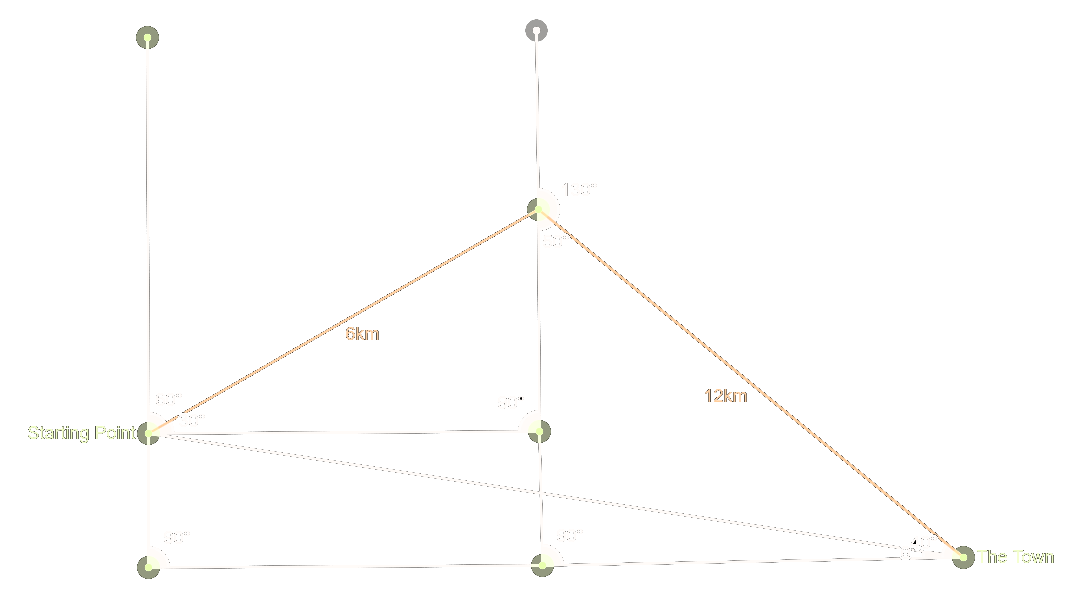
4b. John lost in the desert
John is lost in the desert and he is searching for the nearest settlement. He wanders on a bearing of 60° for 6km and spots a town on a bearing of 130° 12 km away.
- Find how far east the town is from John's starting point. (2 d.p.)
- Find the bearing from John's starting point to the town. (nearest minute)
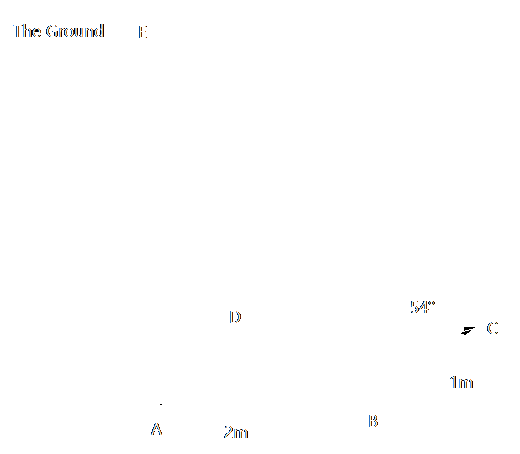
5a. John buried alive
After being assumed dead, John is buried in a local cemetery. However, John is still alive, and he needs to calculate the distance that he needs to climb his way out. John calculates that the hole is 2m wide and 1m long. He also finds that ∠ACE 54°.
If John is 30cm tall, calculate how far he has to claw his way out. (2 d.p.)
5b. John in one final plane crash
After surviving falling off a building, accidentally stabbing himself, a plane crash, falling out of a different plane, being crushed by a grand piano, being accidentally shot by the police, walking many, many hours without food or water and being buried alive...
John finally met his demise after the plane he fell out of earlier crashed into him.
- If the plane (L) aimed for the town instead, how far would it have to fly? (2 d.p.)
- It just so happens that all the town's people had gathered for an event at the place John was buried. How far did they travel from the town? (2 d.p.)
(AF || BE)
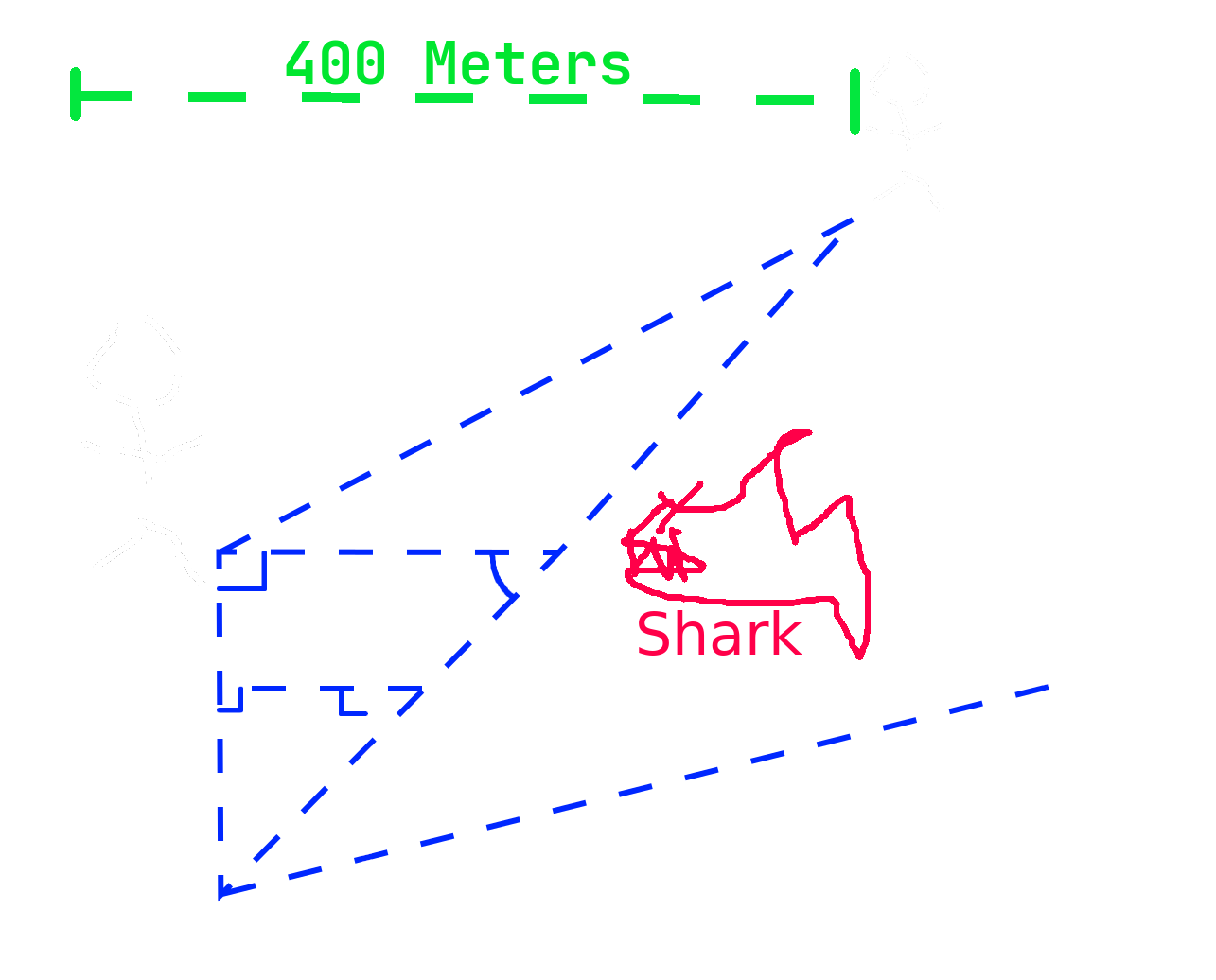
6a. John with a shark
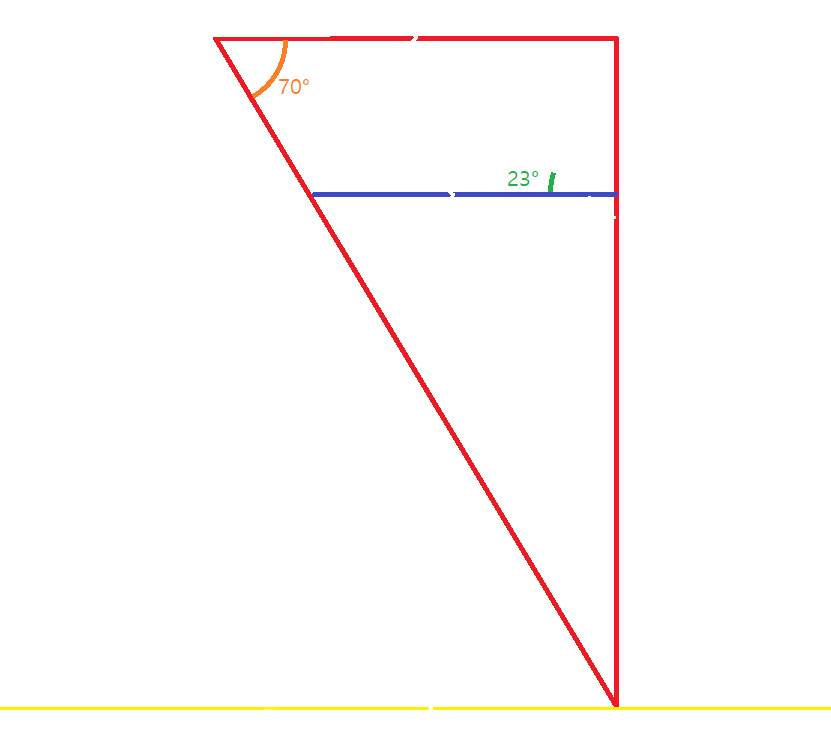
John is having a swim in a pool 80 metres deep and 400 metres long, with points F and G lying flat on the bottom. Suddenly, a shark swims out of a pipe on the floor and stops at point D. John, who is at point B, is also 250 metres from a person at the edge, point A. Point A is 200 metres away from point G, on the bottom of the pool. The horizontal distance between point D and the right side of the pool wall is 120 metres.
- If BF is 40 metres and FG is 50 metres, and the shark swims at the terminal velocity of 89.7m/s, how long will it take to get and eat John?
- John escapes the shark and swims down into the pipe. If he swims down to point C before drowning, and the distance between F and C is 80 metres, how far is John from the shark?
- Right before John drowns at point C, the person at point A drags him up to the surface. However, John slips on the pool tiles and falls 80 metres from point A to point E. If CE is 250 metres long, and angle GCE 32 degrees, and the shark burrows through the wall in 6 seconds (the wall stretches from point D to E), how fast does the shark burrow through the wall to devour John?
6b. John Feeds the Lions
John is feeding the lions at point D. He throws the food to point C and point B, where the lions converge on to eat. Unfortunately, as he is about to leave, he trips on a child’s vomit and falls to point A, in the lion enclosure. John figures there is 33 metres between the lions, and their angle of elevation to point D for C and B is 28 and 42 degrees consecutively.
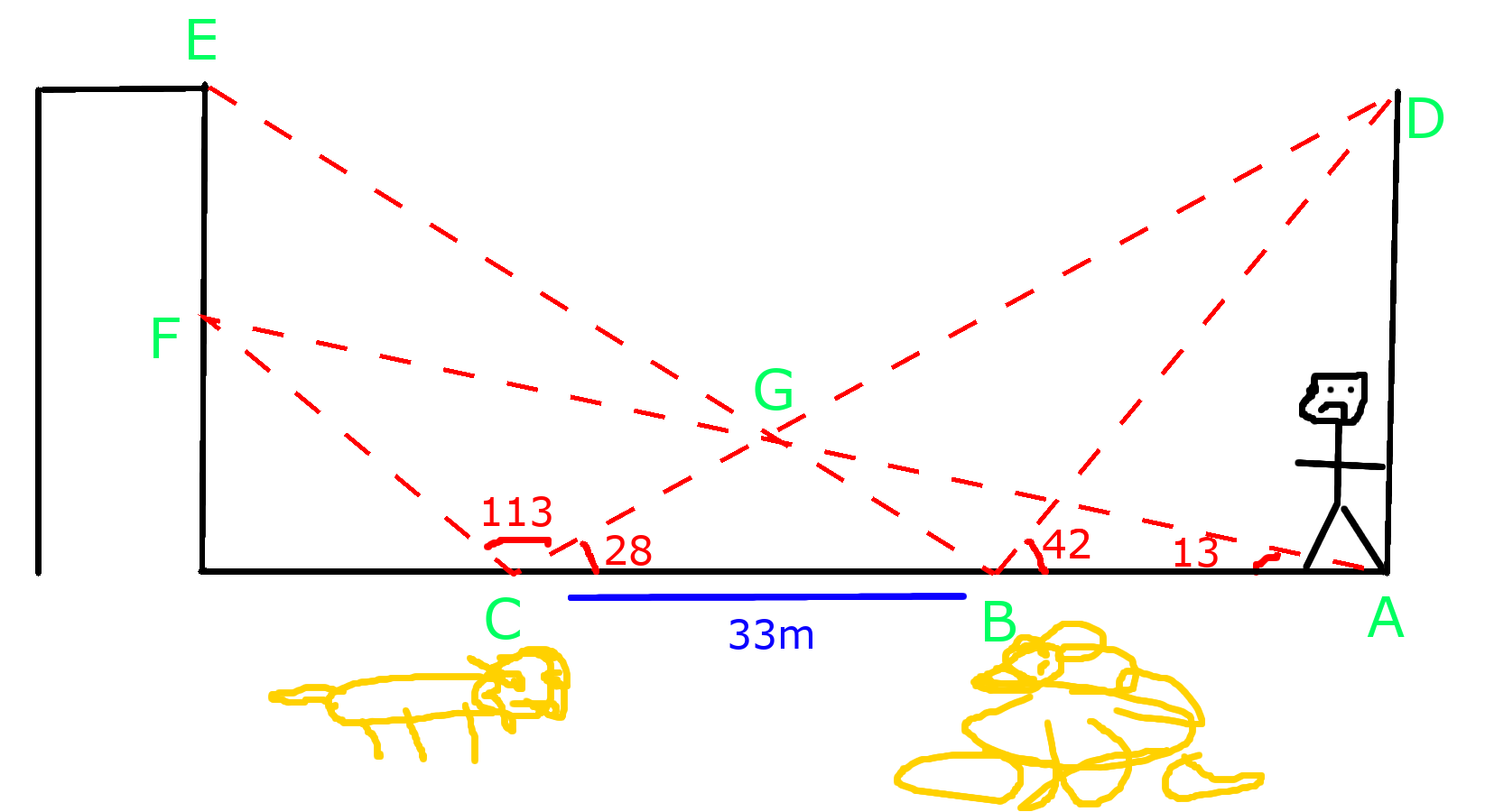
- If John can climb at 12 metres per second, how long will it take for him to get back to the top of the enclosure?
- When John gets to the top of the enclosure at point D, the lions pounce and gnaw his legs off. John is flung to point C. If angle FCG is 113 degrees and angle CAF is 13 degrees, How far will John have to crawl to get to the right angle between F and C?

ANSWERS:
John feeds the crocodilesJohn is feeding the crocodiles in a square enclosure ABCD. He falls into the enclosure, landing at some point E. Let x be the length of the side of the enclosure.
There is a crocodile at point A and point B. Let m and n be the distances between the crocodiles and John, and theta the angle between them.
John calculates that the area of the enclosure is denoted by:
Furthermore, he realises the perimeter of triangle ABE is given as:
a. Find values of m and n, in the form a+bc .
b. The crocodiles decide to smear the triangle ABE with John’s blood. Show that the area of the triangle is:
c. The crocodiles need to paint the floor with 0.25 litres of John’s blood every square metre. Find the maximum amount of blood the crocodiles need.
Question 1
a. John falling off a building
- 351.43m
- 38°
Question 2
a. John in a plane crash — 36°
b. John falling from a plane — 92.2 seconds
Question 3
a. John crushed by a grand piano — 80° 41'
b. John caught in a shootout
- Officer 1 — 2° 36'
- Officer 2 — 29° 33'
Question 4
a. John walking home — 1258.45 hours
b. John lost in the desert
- 14.39 km east
- 108° 8' bearing to town
Question 5
a. John buried alive — 2.78 m
b. John in one final plane crash
- 9.79 km
- 12.04 km
Question 6
a. John with a shark
- 1.263 seconds
- 154 m
- 24.1 m/s
b. John Feeds the Lions
- 3.571 seconds
- 32.139 metres
Question 7
a. m and n can be 10 + - sqrt(11)
c. 7 litres